Tutorial-14: To read the sides of a Triangle and check its shape & perform complete Path Testing on it
Inputs for the Tutorial: A triangle having three sides a, b and c with their values in the range of 0 to 100 as integers.
Objective of this Tutorial: There are two objectives of the tutorial like:
Objective 1: To write a Program in C++ for the checking as to whether the triangle is either of : Equilateral Triangle, Isosceles Triangle, Scalene or “Not a Triangle”.
Objective 2: To perform Path Testing on the above & derive the following:
1) Flow Graph
2) DD Path Graph
3) Independent Paths
4) Cyclomatic Complexity
Solution Part 1: Program in C++
#include
#include
(1) int main ()
(2) {
(3) int a, b, c, validinput = 0;
(4) printf(“Enter the side `a’ value:”)
(5) scanf(“%d”,&a);
(6) printf(“Enter the side `b’ value:”)
(7) scanf(“%d”,&b);
(8) printf(“Enter the side `c’ value:”)
(9) scanf(%d”, %c);
(10) if((a>0)&&(a<100)&&(b>0)&&(b<=100)&&(c>0)&&(c<=100))
{
(11) if(((a+b)>c)&&((c+a)>b)&&((b+c)>a))
{
(12) validInput=l;
(13) }
(14) }
(15) else
}
(16) validInput=-l;
(17) }
(18) if(validInput==1)
{
(19) if((a==b)&&(b==c))
{
(20) printf(“The triangle is EQUILATERAL”);
(21) }
(22) else if((a==b)||(b==c)||(c==a))
{
(23) printf(“The triangle is ISOSCELES”);
(24) }
(25) else
{
(26) printf(“The triangle is SCALENE”);
(27) }
(28) }
(29) elseif(validInput==0)
{
(30) printf(“The values do not constitute a triangle”);
(31) }
(32) else
{
(33) printf(“The inputs belong to invalid range”);
(34) }
(35) getche();
(36) return 1;
(37) }
Solution Part 2:
A) Mapping Table for DD path Graph
| Flow Graph Nodes | DD Path Graph Corresponding Nodes | Remarks |
| 1 to 9 | A | Sequential Nodes |
| 10 | B | Decision Nodes |
| 11 | C | Decision Nodes |
| 12,13 | D | Sequential Nodes |
| 14 | E | Two edges are joined here |
| 15,16,17 | F | Sequential Nodes |
| 18 | G | Decision nodes plus joining of two edges |
| 19 | H | Decision Nodes |
| 20,21 | I | Sequential Nodes |
| 22 | J | Decision Nodes |
| 23,24 | K | Sequential Nodes |
| 25,26,27 | L | Sequential Nodes |
| 28 | M | Three edges combined here |
| 29 | N | Decision Nodes |
| 30,31 | O | Sequential Nodes |
| 32,33,34 | P | Sequential Nodes |
| 35 | Q | Three edges combined here |
| 36,37 | R | Sequential nodes with exit node |
B) Independent Paths
1) ABFGNPQR
2) ABFGNOQR
3) ABCEGNPQR
4) ABCDGIMOQR
5) ABFGHIMQR
6) ABFGHJKMQR
7) ABFGHJLMQR
C) Cyclomatic Complexity
The Cyclomatic Complexity or the Structural Complexity of the above code can be found by using the formulae
V(G) = e – n + 2P
where V(G) is the cyclomatic metric of Graph ‘G’ with ‘n’ vertices, ‘e’ edges and ‘P’ connected components.
In this case, the value of e = 23, n = 18 and P = 1.
Therefore, the value of V (G) comes out to be 7
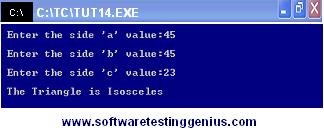
Two sample Screenshot with different output are as under:
Screenshot 1: For an Equilateral Triangle

Screenshot 2: For an Isosceles Triangle
Many More Articles & Tutorials on Black Box Testing

An expert on R&D, Online Training and Publishing. He is M.Tech. (Honours) and is a part of the STG team since inception.
