Download Link for your Favorite Presentation is at the End of this Page
**********************************************************************************
Tutorial-4: Estimation of Complexity Measure V(G): For a Quadratic Equation
Objective of the Tutorial:To draw a Flow Graph, find its Cyclomatic Complexity, V(G) and the independent paths for the program reading a, b and c as the three coefficients of the quadratic equation
aX2 + bx + c = 0. It determines the nature of the roots of this equation.
A brief Introduction to Basis Path Testing & measurement of Complexity Measure V(G):
Basis path testing helps a tester to compute logical complexity measure, V(G), of the code. This value of V(G), defines the maximum number of test cases to be designed by identifying basis set of execution paths to ensure that all statements are executed at least once.
Steps to compute the complexity measure, V(G) are as under
Step 1: Construct the flow graph from the source code or flow charts.
Refer Following Tutorial on :
Flow Graph and its Notations
Step 2: Identify independent paths.
Step 3: Calculate Cyclomatic Complexity, V(G).
Step 4: Design the test cases.
Starting point for the Tutorial: Is the construction of the Flow Graph:
Step 1: Start writing the procedure.
proc roots
(1) int a, b, c;
(2) D = b * b – 4 * a * c;
(3) if (D < 0)
(4) real = -b/2 * a ; // imaginary roots
D = – D;
num = pow ((double) D, (double) 0.5);
image = num/(2 * a);
(5) else if (D = = 0)
(6) root 1 = -b/(2 * a) root 2 = root 1;
(7) else if (D > 0)
(8) root 1 = (-b + sqrt (d)/2 * a;
root 2 = (-b – sgrt(d)/2 * a;
(9) end
Step 2: Draw the following Flow Graph
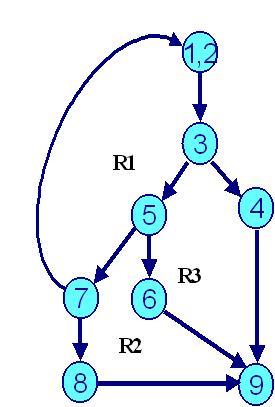
Step 3: Calculation of Cyclomatic Complexity V(G) by three methods
Method 1: V(G) = e � n + 2 ( Where �e� are edges & �n� are nodes)
V(G) = 11� 9 + 2 = 2 + 2 = 4
Method 2: V(G) = P + 1 (Where P � No. of predicate nodes with out degree = 2)
V(G) = 3 + 1 = 4 (Nodes 3, 5 & 7 are predicate nodes with 2 outgoing edges)
Method 3: V(G) = Number of enclosed regions + 1 = 3+1=4
( Here R1, R2 & R3 are the enclosed regions and 1 corresponds to one outer region)
V(G) = 4 and is same by all the three methods.
Step 4: Identification of the basis-set with four paths
| Path 1: | 1 � 2 � 3 � 4 � 9 |
| Path 2: | 1 � 2 � 3 � 5 � 6 � 9 |
| Path 3: | 1 � 2 � 3 � 5 � 7 � 8 � 9 |
| Path 4: | 1 � 2 � 3 � 5 � 7 � 1 � 2 ��. |
Conclusions from the above tutorial:
The test cases for each of the path are:
Path – 1: Test case 1
a, b, c : valid input
Expected results: D < 0, imaginary roots
Path – 2: Test case 2
a, b, c : valid input
Expected results: D = 0, equal roots
Path – 3: Test case 3
a, b, c : valid input
Expected results: D > 0, root 1 and root 2 are real.
Path – 4: Test case 4
a, b, c : valid input
Expected results: D is not > 0, read a, b, c again
Many more Articles & Tutorials on White Box Testing
DownLoad Link for Presentation:
How to Run a Scenario in HP LoadRunner (386 Kb)
