Tutorial-6 DD Path Testing Case of a Quadratic Equation

Posted in: White Box Testing

Tutorial-6: DD Path Testing: Case of a Quadratic Equation

Objective of the Tutorial: To draw a Flow Graph, a DD Graph, calculation of Cyclomatic Complexity V(G) and find out all independent paths from the DD paths graph, for the case of quadratic equation ax² + bx + c = 0 where three coefficients a, b and c roots are calculated. The output may be real roots, imaginary roots or equal roots or even the equation may not be a quadratic equation.

When we have a flow graph, we can easily draw another graph that is known as decision-to-decision or (DD) path graph, wherein we lay our main focus on the decision nodes only. The nodes of the flow graph are combined into a single node it they are in sequence.

Process of constructing the DD Graph leading to computation of Cyclomatic Complexity goes like this:

Step 1: Start writing the following program

# include

(1) int main ( )

(2) {

(3) int a, b, c, d, boolean = 0;

(4) double D;
(5) printf (�nt Enter `a’ coefficient :”);

(6) scanf (“%d”, & a) ;

(7) printf (“nt Enter `b’ coefficient :�);

(8) scanf (“%&d”, & b);

(9) printf (�nt Enter `c’ coefficient :�);

(10) scanf, (“%d�, & c) ;

(11) if ((a > =0) && (a < = 00) && (b > = 0) && (b < =100) && (c > =0) && (c < =100)) {

(12) boolean = 1;

(13) if (a = = 0) {

(14) boolean = -1;

(15) }

(16) }

(17) if (boolean = = 1) {

(18) d = b * b � 4 * a * c;

(19) if (d = = 0) {

(20) printf (“roots are equal and are r1= r2 = %f – b/(2 * float)&));

(21) }

(22) else if (d > 0) {

(23) D = sqrt (d);

(24) printf (“roots are real and are r1=%f and r2=%f; (-b – D)/(2 * a), (-b + D)/(2 * a));

(25) }

(26) else {

(27) D = sqrt (-d) / (2 * a);

(28) printf (“roots are imaginary”);

(29) }

(30) }

(31) else if (boolean = = -1) {

(32) printf (“Not a quadratic equation”);

(33) }

(34) else {

(35) printf (“Invalid input range …);

(36) }

(37) getch ( ):

(38) return 0;

(39) }

Step 2: Draw the following Flow Graph

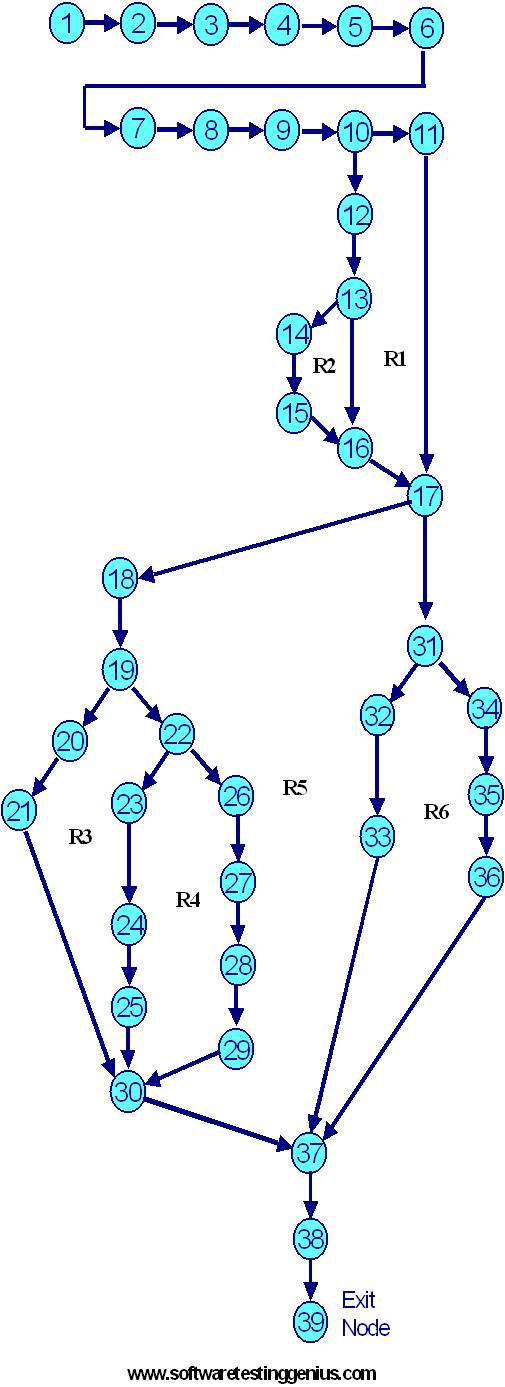
Flow Graph

Step 3: Draw the following DD Path Graph

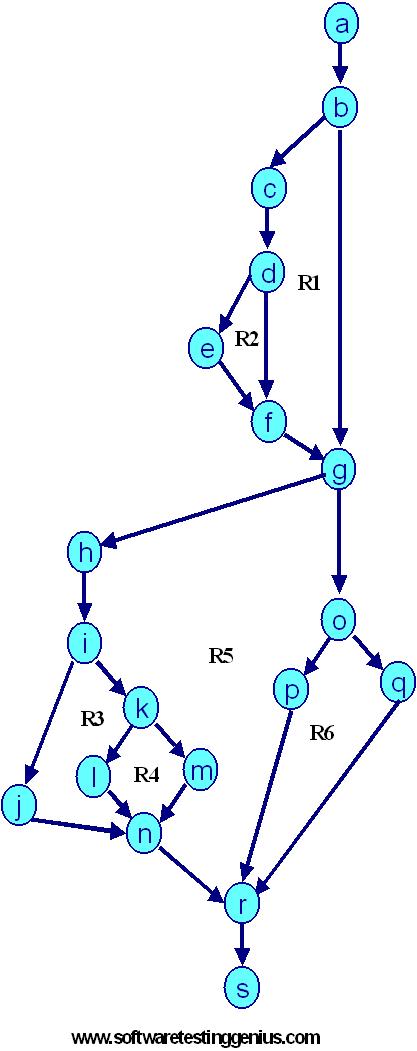
Since, nodes 1-10 are sequential nodes in the above flow graph, hence they are merged together as a single node � �a�.

Since node ��11� is a decision node, thus we cannot merge it any more.

Likewise we can go on deciding the merging of nodes & arrive at the following DD Path Graph

We get following decision table.

Nodes in Flow Graph	Corresponding Nodes of DD Path Graph	Justification
1- 9	a	Are Sequential Nodes
10	b	Decision Nodes
11	c	Decision Nodes
12, 13	d	Sequential Nodes
14	e	Two Edges Combined
15, 16, 17	f	Sequential Nodes
18	g	Decision Nodes
19	h	Decision Nodes
20, 21	i	Sequential Node
22	j	Decision Node
23, 24	k	Sequential Node
25, 26, 27	I	Sequential Nodes
28	m	Three Edges Combined
29	n	Decision Node
30, 31	o	Sequential Node
32, 33, 34	p	Sequential Nodes
35	q	Three edges Combined
36, 37	r	Sequential Exit Nodes

Step 4: Calculation of Cyclomatic Complexity V(G) by three methods

Method 1: V(G) = e � n + 2 ( Where �e� are edges & �n� are nodes)

V(G) = 24� 19+ 2 = 5 + 2 = 7

Method 2: V(G) = P + 1 (Where P � No. of predicate nodes with out degree = 2)

V(G) = 6 + 1 = 7 (Nodes d, b, g, I, o & k are predicate nodes with 2 outgoing edges)

Method 3: V(G) = Number of enclosed regions + 1 = 6+1=7
( Here R1, R2, R3, R4, R5 & R6 are the enclosed regions and 1 corresponds to one outer region)

V(G) = 7 and is same by all the three methods.

Step 5: Identification of the basis-set with Seven Paths

Path 1:	a � b � f � g � n � p � q � r
Path 2:	a � b � f � g � n � o � q � r
Path 3:	a � b � c � e � g � n � p � q � r
Path 4:	a � b � c � d � e � g � n � o � q � r
Path 5:	a � b � f � g � h � i � m � q � r
Path 6:	a � b � f � g � h � i � k � m � q � r
Path 7:	a � b � f � g � h � j � l � m � q � r